1.618033988749894

El acato de las reglas conduce muchas veces a la recompensa: del galardón más público a la satisfacción menos evidente, los honores sobrevienen si las obras lo merecen. Hay ocasiones, sin embargo, que el mérito no es otro que confirmar el funcionamiento de un sistema, en cuyo caso, la recompensa llega a ser, extrañamente, la belleza.

Por: Rafael Arce y De la Borbolla ¹

De Broglie y el Modelo Estándar (1927)

“Dios no juega a los dados con el Universo”.
(Albert Einstein)

El modelo de De Broglie había fracasado. Se prefirió el modelo irracional, azaroso y desordenado de Bohr, la incertidumbre de Heisenberg y el gato de Schrödinger. Parecía que la ciencia voluntariamente estaba regresando a la caverna platónica donde hay cosas que simplemente no se pueden saber. Sí, es cierto que existe la dualidad onda-partícula (que, según el experimento, se aprecian unas u otras propiedades), pero dejarlas al azar o establecer que “un gato está vivo y muerto al mismo tiempo, pues no se sabe con exactitud el estado del gato” le parecía un absurdo. El modelo de De Broglie corroboraba —con bastante precisión, cabe mencionar— que la mecánica cuántica tiene reglas racionales y causalmente determinadas, pero también era innegable que, para los valores filosófico-sociales de 1920, eran mucho más atractivas y elegantes las fórmulas de Schrödinger o de Heisenberg que el postulado de De Broglie, además de que éste también se servía de las fórmulas de aquellos. Pero los resultados no engañan: experimentos a gran escala siguiendo la teoría de la “onda piloto” resultan, probabilísticamente hablando, en modelos similares a los formulados por el principio de incertidumbre. 

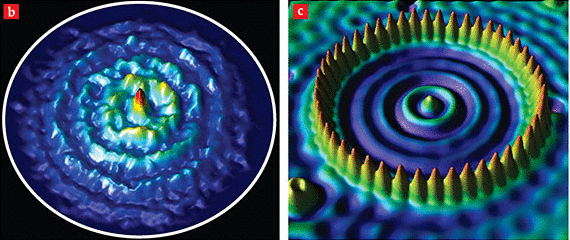
Imagen 1: Dos modelos fundamentalmente opuestos, la Teoría de la onda Piloto y el Modelo Estándar, generan imágenes similares de un patrón de partículas (gotas o electrones) y ondas.
Fuente: quora.com

Napoleón y el sistema métrico decimal (1800)

La monarquía perdió la cabeza y Francia perdió a su monarquía. Eran tiempos caóticos y, sin embargo, se encomendó a Jean-Baptiste Joseph Delambre y Pierre Méchain que fueran desde Montjuic, en Barcelona, hasta Dunkerque sacando medidas del meridiano de París con la única finalidad de dar muerte a todos los sistemas de medición de la época. Habían funcionado —más o menos— las varas, los codos, los pies, los brazos o las pulgadas para comerciar y construir. Pero el sistema no era suficientemente bueno, pues no se sabía si las varas eran castellanas o aragonesas, si los pies de uno eran más grandes que los del otro, si las millas eran náuticas o terrestres. Era la hora de dar muerte a esos sistemas. Por eso, en medio de la inestabilidad política de Francia, Delambre y Méchain buscaban la medida para sustituir todas las medidas. 

Así nació el metro y le siguió el litro (1 dm3) y el kilogramo (1 litro), sustituyendo una plétora de medidas que habían sido sobrepasadas por las necesidades humanas. La práctica base 10 sustituyó a la base 12 o a la base 60, pues era más intuitiva para contar con los dedos de las manos. Integraba, además, por medio de un punto, los decimales para expresar fracciones. El sistema parecía que podía englobar todo el lenguaje matemático. Sólo los ingleses y su equivalente americano —en su barbarie natural— se rehusaron a adoptar el sistema nuevo. Pareciera que, por tratarse de una isla, las buenas ideas, como el Renacimiento y la Ilustración, no pudieron llegar como al resto del mundo. 

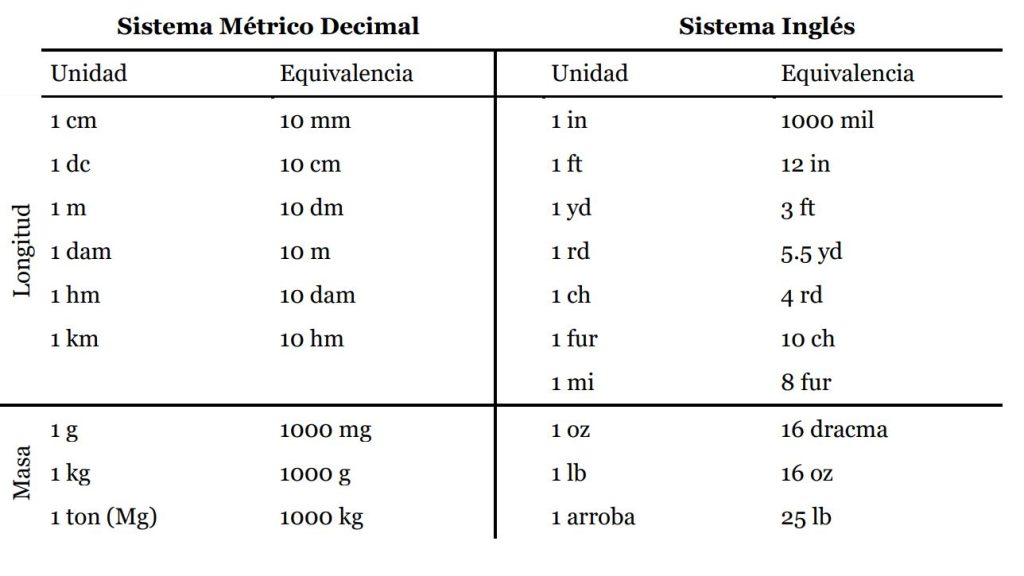
Imagen 2: Dos sistemas métricos, en que la evidente regularidad del primero (métrico) deviene en el rechazo, casi universal, del segundo (anglosajón).

Kepler y los modelos astronómicos (1609)

“Y es que en el mundo traidor,
nada es verdad ni mentira,
todo es según el color
del cristal con que se mira”.
(Ramón de Campoamor)

El modelo kepleriano daba santa sepultura al modelo ptolemaico, que había regido desde el siglo II d.C. Si bien fue Copérnico quien propuso un modelo heliocéntrico, fue Kepler quien daba respuesta a todas las cuestiones técnicas de los movimientos planetarios observados por Brahe. Y no es sólo que haya sustituido los epiciclos, los deferentes y los ecuantes, sino que lo hacía de una forma mucho más simple, mucho más elegante: sus órbitas elípticas alrededor del Sol justificaban, en un solo modelo —sin excepciones ni reglas particulares—, las estaciones del año, los periodos de los cuerpos celestes y —¿por qué no?— sus retrógrados. 

No es que el modelo ptolemaico, que con círculos concéntricos describía los movimientos de los cuerpos celestes alrededor de la Tierra, no funcionara —funcionó por 15 siglos, es decir, mil años más que lo que ha durado el heliocéntrico—, pero necesitaba de algunas excepciones como los epiciclos y los ecuantes que terminaban por ensuciar el modelo. En lo que a nosotros concierne, el modelo de Kepler requiere una cantidad menor de justificaciones que no sólo atiende a los planetas, sino que es aplicable a otros cuerpos celestes cuyos periodos  traslacionales eran mucho mayores, como los cometas. 

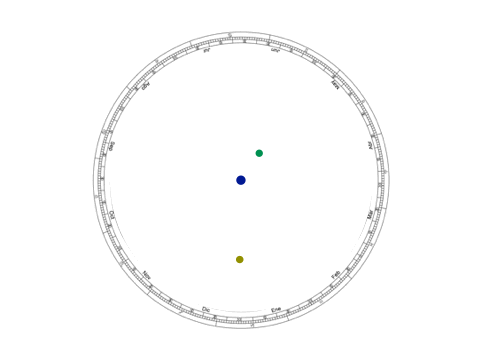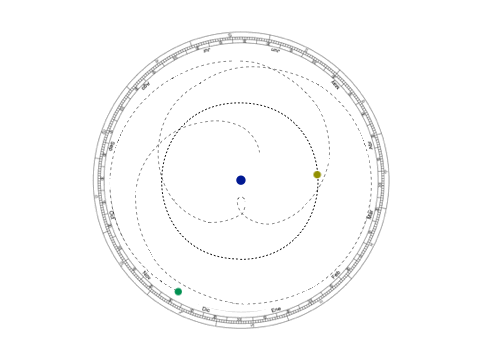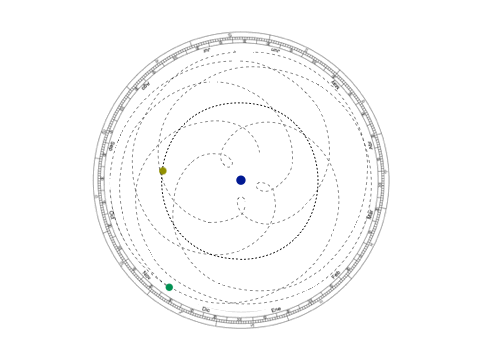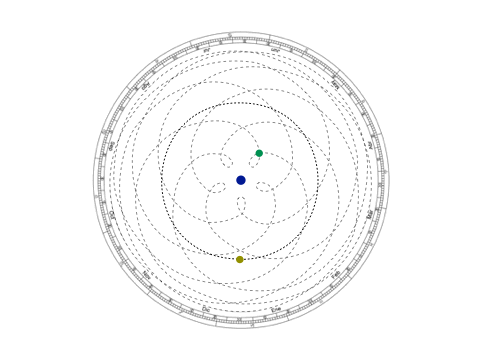
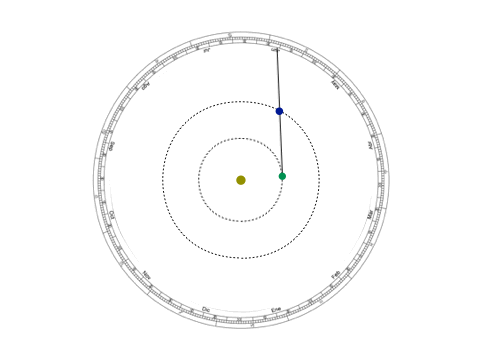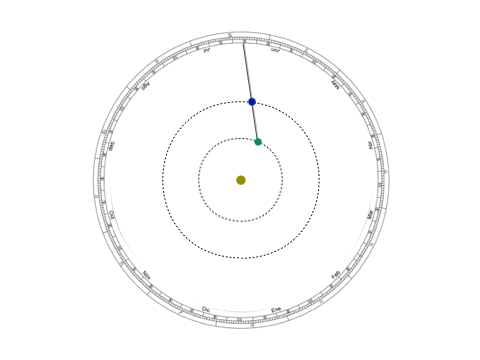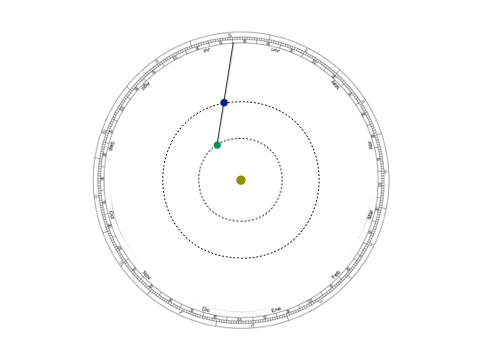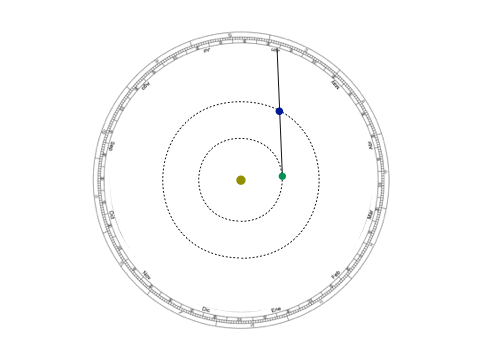
Imagen 3: Modelo geocéntrico y kepleriano de la retrogradación planetaria. En el primero, las órbitas del Sol y de Venus se cruzan, además de tener un acercamiento muy marcado hacia la tierra.

Hildegarda y las escalas musicales (1179)

A Pitágoras se le atribuye haber descubierto que las octavas musicales tenían una proporción de dos a uno (2:1) en una cuerda previamente tensada. De este descubrimiento vienen todas las escalas musicales. Los griegos basaron su música en modos —también llamados “armonías” o “tonos”—, que consistían en descender una nota dominante mediante dos tetracordios, por ejemplo: Do – Re – Mi – Fa y Sol – La – Si – Do. Fueron los monjes del medioevo, entre los que destaca Hildegarda de Bingen, quienes desarrollaron un sistema de escritura que representaba gráficamente cualquier obra musical. En este sistema se establecieron los tiempos y los tonos de las notas que debían seguir los músicos. Fueron los mismos monjes quienes descubrieron que hay una relación eufónica entre varias notas que, al combinarse, suenan bien. Eso fue muy importante, ya que la música en el medioevo era coral y requerían una unidad armónica. Los cantos gregorianos eran muestra de esa necesidad de armonía entre las distintas voces de tonos diferentes. A este conjunto se le conoce hoy como “acorde”, y es fundamental en cualquier academia de música su enseñanza.  

Gracias a estos descubrimientos, la música occidental pudo dar un salto importante con la llegada de J. S. Bach, quien entendió, como nadie antes, los diferentes juegos que generan las notas y de paso abrió las puertas para que los compositores posteriores lograran obras cada vez más ambiciosas.  

Por supuesto que la notación creada por los monjes medievales no es música, pues la ésta sólo existe en sonido. En papel, en cambio, no es más que una representación de la realidad: sencillamente, sólo es su medio. Pero esa representación y ese entendimiento de voces son lo que han logrado expresar todas las piezas musicales que se han compuesto en la humanidad. 

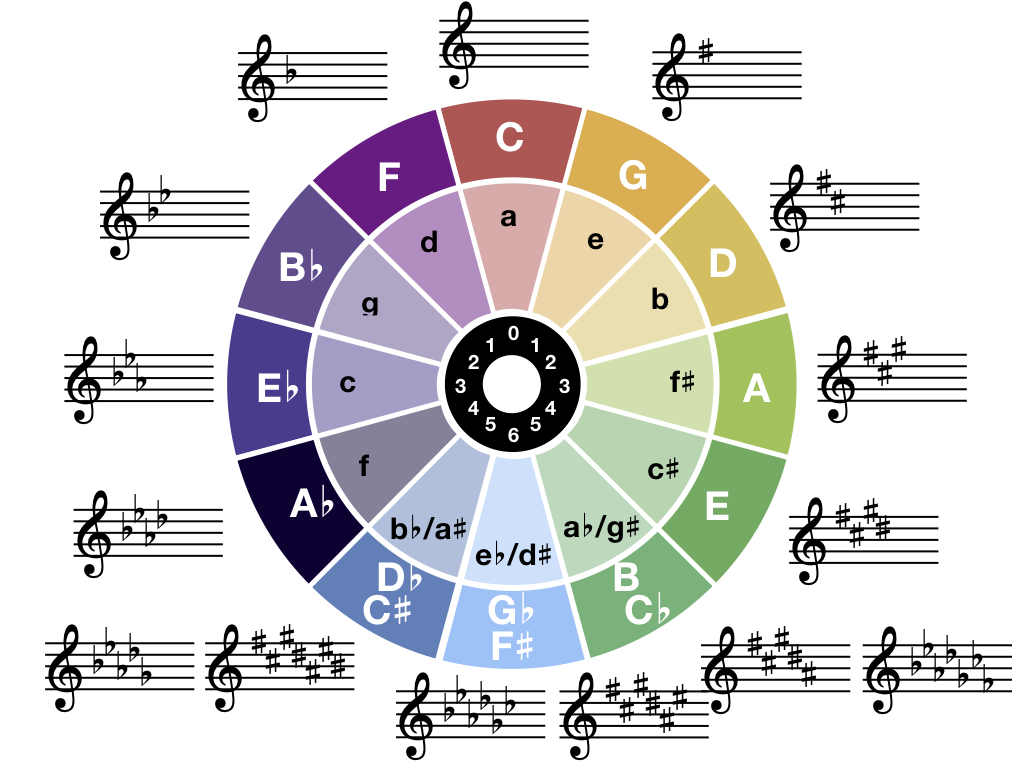
Imagen 4: El círculo de quintas representa gráficamente las 12 tonalidades mayores (círculo exterior) y menores (círculo interior). El modelo marca las armaduras, los acordes, las pentatónicas y armonizaciones, condición que lo vuelve muy superior a los limitados modos griegos.

Al-Jwarizmī y los lenguajes numéricos (820)

A Al-Jwarizmī se le atribuye la introducción del sistema arábigo de numeración a occidente, una serie de grafemas extraños que parecían decir poco de las cantidades que querían expresar, pero que funcionaban cual brujería: según la posición de esos 10 grafemas, se pueden expresar todas las cantidades conocidas, y no sólo hasta MMMCMXCIX. Si se les hacían operaciones aritméticas, también funcionaban sobre esos símbolos. Inclusive, eran buenos para las multiplicaciones y las divisiones.  

Algunos dicen que estos símbolos, como cualquier sistema decente de numeración, contaban ángulos. Si es cierto o no, no importa, pues cuentan absolutamente todo en todos los infinitos posibles: fracciones, decimales, imaginarios, reales, naturales. Gracias a ellos, podemos cambiar las bases a binario o hexadecimal sin perder certeza, se inventaron los algoritmos (palabra que procede del nombre de Al-Jwarizmī latinizado) y se resolvieron numéricamente todos los teoremas. Además, sin ellos, ni Newton ni Leibnitz hubieran podido inventar el cálculo. 

No es de extrañar que haya sido una cultura árabe la que hayan logrado componer este sistema, pues, en esa región, la escritura se inventó para contar y sus mentes tienen predisposición para los cálculos, posiblemente por ser el cruce comercial de tres continentes. Una de las razones de que la comunidad judía sea tan exitosa en los negocios es que su propio lenguaje guarda relaciones numéricas. 

Imagen 5: Diferentes lenguajes numéricos: arábigo, romano, maya y griego. Tanto el griego como el romano parecen no llevar cuentas, al contrario del maya y el arábigo —si resultase cierta la teoría de que este último cuenta ángulos (marcados con puntos rojos)—.

Pitágoras y los modelos geométricos (490 a.C.)

De entre las grandes aportaciones que hizo Pitágoras, además de aquellas en la música, están algunas en las matemáticas. Él, junto con un grupo de seguidores, descubrió relaciones entre los números, el cosmos, la astronomía y la música, elevando los modelos numéricos sobre el uso exclusivo de cuentas para los comerciantes. A este avance hay que entenderlo de la manera como lo veían los pitagóricos, pues, como ya describimos antes, no existían los puntos decimales ni contaban con numerales aptos para hacer operaciones aritméticas de manera sencilla. Su única herramienta era la geometría.  

Los griegos descubrieron, a través de la geometría, muchas cosas: que un triángulo inscrito en un semicírculo siempre es rectángulo; que la suma de los ángulos internos de un triángulo siempre es igual a dos ángulos rectos (180º); que el perímetro de un círculo, independientemente de su tamaño, siempre es tres veces y fracción su diámetro; que hay números que no se pueden expresar como cocientes de dos enteros, a los que llamaron “inconmensurables” —hoy se llaman “irracionales”—, a partir de triángulos rectángulos. 

Por supuesto, Pitágoras obtuvo muchas de sus ideas y su visión matemática de otras regiones, como Egipto, Arabia y Fenicia. Ejemplo de esto es el famoso triángulo egipcio: un triángulo de lados 3, 4 y 5, que, además de tener la gracia de que los lados sean números enteros consecutivos, tiene la función de hacer escuadra de 90º, una propiedad muy útil para la construcción, pues permite edificar aprovechando al máximo el espacio y formando retículas perfectas. Pero lo que lograron los pitagóricos fue sistematizar todo el conocimiento geométrico y demostrar algunas proposiciones. De esa manera, lograron expresar que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. De nuevo, esa demostración se logró sin involucrar operación matemática alguna, sino con figuras puramente geométricas, siendo el cuadrado de un cateto no la multiplicación del lado por sí mismo, sino la construcción literal de un cuadrado. 

Imagen 6: Imagen de cómo se aplican varios principios geométricos descubiertos por los pitagóricos: a) todo triangulo inscrito en un semicírculo es rectángulo; b) el triángulo egipcio es rectángulo con lados 3, 4 y 5; c) el teorema de Pitágoras cumple con que la suma de los cuadrados de los catetos es igual al cuadrado de la hipotenusa. Finalmente, como curiosidad, un círculo inscrito en ese triángulo tiene un área igual a π y una circunferencia igual a 2π.

Fibonacci y las series proporcionales (1240)

Posiblemente, el mejor matemático de la Europa medieval fue Leonardo de Pisa —también conocido como “Fibonacci”—, quien se encargó de difundir el sistema arábigo de números en el continente europeo. Gracias a que su padre era comerciante con negocios en Argelia, Leonardo entendió el sistema arábigo de numerales y lo aplicó para establecer lo que hoy se conoce como “serie de Fibonacci”: 0, 1, 1, 2, 3, 5, 8, 13, 21… etcétera.  

Fibonacci creó esta sucesión numérica infinita sumando los dos números anteriores para descubrir el siguiente en la serie. Esta serie cuenta con algunas propiedades interesantes. Una de ellas es que, si se divide uno de sus números por su anterior, se va aproximando al número áureo (φ), que los griegos consideraban propio de la belleza. No es para menos, pues, sorprendentemente, el sistema está contenido en sí mismo. Recordemos que los griegos no conocían el punto decimal y no era posible expresar un número irracional con fracciones de números enteros, por lo que es muy probable que los mismos griegos usaran alguna versión de la serie de Fibonacci. 

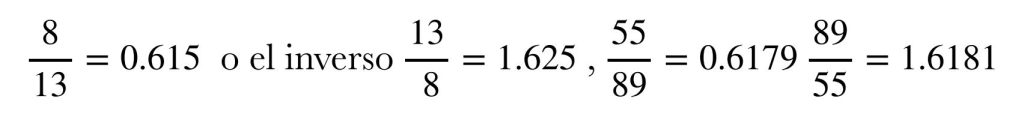
Además, la serie Fibonacci aplica para cualquier sucesión de números que siga la regla de sumar los dos anteriores para encontrar el siguiente, por ejemplo: si se empieza, con el 37 y luego el 213, dentro de 15 números, la división entre dos cifras consecutivas se irá aproximando cada vez más al 1.6180… ó 0.6180…

Imagen 7: Se aprecia geométricamente la serie de Fibonacci: segmentos del pentagrama, otro pentagrama dentro del inicial pentagrama, el cuadrado y el triángulo áureo y las espirales resultantes.

Venus y los modelos de la Belleza

¿Existe la Belleza? Es extraño que, para tratar a la Belleza, se empiece por un viaje histórico de sistemas numéricos y modelos científicos, pero la tesis —por extravagante que parezca— lo requiere y lo amerita. Claro que existe la Belleza, pero da la impresión de que depende no tanto del objeto a quien se le atribuye la característica, sino del espectador: que lo bello para uno no necesariamente lo es para otro; que, a diferencia de cuestiones científicas, la Belleza no da valores verdaderos o falsos…finalmente, que no hay una Belleza Universal.  

Los griegos pensaban diferente: según Platón, era una presencia del mundo inteligible en el mundo sensible, de la que no era posible dudar; según Aristóteles, era algo valioso por sí mismo y no por su utilidad; según Fidias, estaba más relacionada con la proporción áurea. De nueva cuenta, parece que tantas opiniones sólo confirman la subjetividad de la Belleza.  

La intención de mostrar varios modelos y sistemas al principio del texto es enfrentar dos posturas donde hay un claro vencedor: el modelo estándar para la física cuántica, el sistema métrico decimal para medidas, el modelo kepleriano para las órbitas planetarias, la notación musical medieval o los numerales arábigos. Todos estos sistemas no sólo atienden problemas puntuales de su tiempo, sino que, con el paso de los años, siguen vigentes y funcionan para cuestiones descubiertas o inventadas posteriormente (cometas, satélites, asteroides; números decimales, irracionales, imaginarios;² música clásica, jazz, reggaetón). Es importante mencionar que ninguno de estos modelos son la realidad, sino meras interpretaciones —por ejemplo: la música sólo existe en sonido, y su medio de apreciación es el oído, no la partitura—, por lo que es igual de válido contar con numerales mayas que con arábigos, pero estos son mejores para expresar más cosas, no sólo contar. Podemos decir, objetivamente, que un sistema es mejor que otro. 

Pasa lo mismo con la Belleza: objetivamente hay cosas mejores que otras, pero hay otros factores que influyen al momento de catalogar algo como bello: existe un filtro personal y subjetivo llamado gusto —de ahí que la gente prefiera escuchar Callaita de Bad Bunny al Concierto para piano, Op. 17 de Jan Paderewski—³ o un mismo objeto puede caer en varios sistemas y tener propiedades diferentes en cada uno de ellos. Pero la Belleza sigue siendo objetiva, y lo es en cuanto a un sistema.  

Regresando con los griegos, que descubrieron la proporción áurea, no significa que ésta sea bella por sí misma o que sea agradable al ojo humano, sino que es un sistema bello, pues está contenido en sí mismo. Ya sea 1.618033988749894 o, lo que es lo mismo, 1 1 2 3 5 8 13 21 34 55 89 144⁴ —de ahí el título del artículo—, las proporciones del rectángulo áureo siempre son las mismas y además está contenido en sí mismo. Pasa lo mismo con el pentagrama y el triángulo áureo. A los griegos les resultaba imposible equivocarse siguiendo la proporción divina, pues, sin importar el espectador, el objeto cumplía con unas reglas preestablecidas que trabajaban en escalas y ámbitos diversos. Podríamos decir que un objeto es bello cuanto más cumpla con las reglas de un sistema. Y un sistema es bello mientas sus reglas se cumplan, aún más allá del propósito para que haya sido creado.  

Posiblemente, como en los modelos científicos, no hemos desarrollado un sistema que englobe todas las bellezas en un mismo modelo, de igual manera que los científicos no han encontrado una teoría que englobe las cuatro fuerzas del universo bajo un mismo modelo, pero puede ser solamente cuestión de tiempo… por lo pronto, yo me atengo al sistema clásico en el que Paderewski es mejor que Benito Martínez. 

1. Geómetra y coleccionista mexicano. ↩︎
2. Los infinitos números arábigos superan a los 3,999 números romanos, al complejo conteo maya o a los inoperantes números griegos.  ↩︎
3. Intencionalmente, se compara a uno de los artistas contemporáneos más populares contra un compositor polaco poco conocido. ↩︎
4.  La representación en numeración decimal y en serie de Fibonacci son dos formas de expresar lo mismo. ↩︎

Nota: las imágenes 2, 6 y 7 fueron elaboradas por el autor. La fotografía de la portada fue obtenida del sitio web de Pexels y los créditos autorales corresponden a Christian Thöni [https://thoeni.design].

Formas críticasRafael Arce y De la Borbolla